芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟_社会万象_知识

芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟

runsly

01-06

0次

古希腊哲学家芝诺其实提出了不少的悖论，其中最著名的四个分别是二分法悖论、阿基里斯悖论、飞矢不动悖论以及竞走悖论，这些悖论几乎都是想要争论世界上的时空到底是可分的还是不可分的，如果可分，那么第一和第三个悖论就无法解决，而如果空间是不可分的，则第三个无法解决。

芝诺悖论是什么

1. 二分法悖论

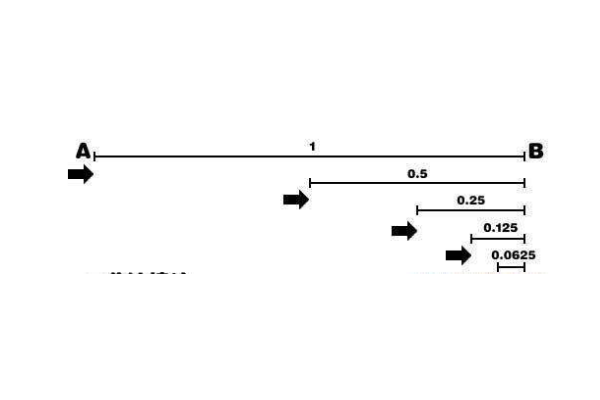
如果假设一个人从A走到B，那么他就一定要通过中心点C，而如果他要从A走到C，那么就一定要通过中心点D，而以此类推下去，那么也就意味着他不管怎么走，都必须要走到中心点，但中心点也就意味着他一定会距离终点有一定的距离，因为哪怕这段距离再小也能找到中心，所以这就使得他形成了一个永远也走不到终点的神奇悖论。

2. 阿基里斯悖论

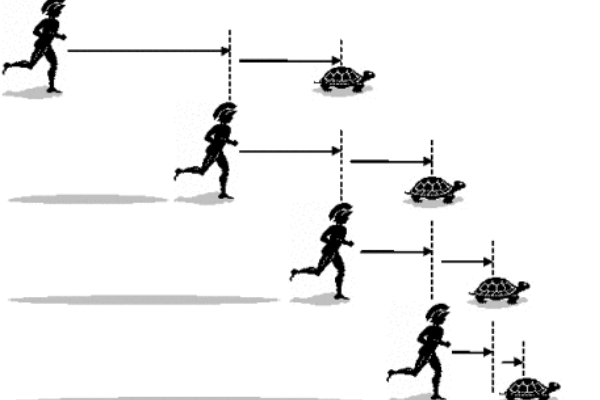
假设古希腊跑的最快的人阿基里斯和一只乌龟进行赛跑，那么首先他就要追上乌龟跑过的第一个位置，当他到位之后，乌龟这时就已经走到第二个点，那么以此类推下去，阿基里斯几乎永远也没有可能追上乌龟，但实际上这时不可能的，因此便形成了第二个悖论。

3. 飞矢不动悖论

当一只箭射出之后，人们看起来它是运动的，但飞箭在某一个瞬间实际上又是不动的，那么人们就会陷入一种飞箭动与不动的争论之中，因此这一悖论就是和“运动可分”这一观点相联系的。

4. 竞走悖论

这一悖论的前提也是时空是有限可分的，假设有三个点A、B、C，其中C向着右边移动，而A向着左边移动，它们的速度对于B来说就是每瞬间移动一个点，而这就意味着A的每点在每个瞬间都会离开C两个点移动的距离，从而我们就能将其无穷化，最终就得出了时间不可分的结论，与前提冲突。

芝诺悖论是什么

上一篇：被推翻的理论：用进废退(拉马克提出被达尔文进化论推翻）

下一篇：火山毒蛛存在吗火山毒蛛是怎么形成的（虚幻电影生物）

芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟

芝诺悖论是什么

相关内容

热门资讯